Flat earth conspiracy theorists have become a loud (if not very large) group since the turn of the millennium. While there are many specific arguments for a flat earth, which are not worth debunking here, all such arguments rely on an underlying principle that one’s senses are trustworthy and we should believe that things are as they appear unless we have strong evidence to the contrary. YouTuber Hbomberguy calls this “direct realism” in his excellent video analyzing the flat earth movement (this direct realism is similar to but not to be confused with what I call naïve realism).

While it is not at all necessary to entertain the prospect of a flat earth, I think it can be useful. While the strongest evidence against a flat earth is undoubtedly the scientific theories that accurately describe and predict many things in the world, this form of evidence isn’t acceptable to flat earthers. Instead, let’s try to refute flat earthers on their own terms. If you were asked to prove that the earth is spheroid using only your own senses, how would you approach it? I encourage you to think about this question.

I would point to the thing that likely first clued in ancient people to the fact that the earth was round like a ball: shadows on the moon. I didn’t understand this the first time it was explained to me, so I want to give a good explanation here.

First, note that geocentrism is a separate issue. For our present purposes, we can grant geocentrism, because making the explanation work in a heliocentric model just involves a shift in frame of reference. In other words, I’m going to talk about the sun and moon as if they go around the earth, but what I am describing is scientifically accurate. Likewise, it is not important for this argument whether the earth rotates or if celestial objects revolve around the earth.

Understanding the movements of the sun, moon, and stars

We’ll ignore planets since they’re not relevant to the present argument.

The sun, moon, and stars move in patterns that can be easily identified by simple observation. Ancient people developed a strong understanding of these patterns long before anything else was known about these celestial bodies.

In the day-night cycle, the sun, moon, and stars all move across the sky from east to west at close to the same speed. The moon’s phase and position at a given hour changes from night to night, and cycles every lunar month (a little over 27 days). The sun’s position also changes from day to day, completing a cycle each solar year (about 365.25 days). Finally, the stars too change their path across the sky slightly from night to night, also completing a cycle once a year but not moving in exactly the same way as the sun.

Eclipses are also predictable, but more difficult to predict. There are 2 to 5 solar eclipses on the earth every year, but at any particular location on the earth solar eclipses may be extremely infrequent (with even partial eclipses often only occurring maybe once or twice in a lifetime). By comparison, a person can generally witness several total lunar eclipses from the same location during their lifetime.

Understanding shadows

We can, like early humans, easily use sunlight and shadow with small objects to understand how shadows work.

First, it is most obvious that when a solar eclipse occurs, the earth is in the shadow of the moon, which is straightforwardly blocking the sun’s light by the moon being an opaque object. This also establishes that the moon is (at least sometimes) nearer to the earth than the sun is.

Next, whether the earth is flat or not, we can consider where the sun, moon, and stars would be if we assume they go all the way around the earth in a circle (note that flat earthers do not believe this, claiming the sun and moon are instead perpetually above the plane of the earth).

Now, when a lunar eclipse occurs, we can determine based on the time and the moon’s position in the sky that the sun would be located directly on the opposite side underneath the earth. Additionally, the motion of the shadow across the moon moves in the correct direction to be caused by the sun beneath the earth casting the earth’s shadow on the moon. Given that no better explanation of lunar eclipses has ever been offered by flat earthers, this is very strong evidence that lunar eclipses are in fact caused by the earth’s shadow.

Once this has been established, the shape of the earth’s shadow reveals it must be spherical. This is because lunar eclipses occur at different locations in the sky, and the earth’s shadow is completely circular in every case. A sphere is the only shape that casts a circular shadow from every direction. If the earth were a disk, the shadow would frequently be foreshortened and appear elliptical rather than circular.

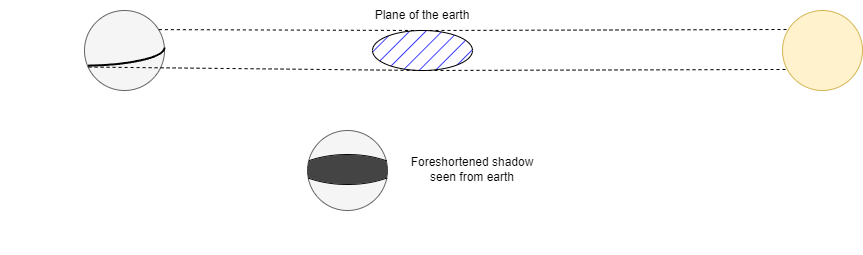
What this argument doesn’t say

Importantly, this concludes only that earth’s shape is spheroid rather than planar and that lunar eclipses must be caused by earth’s shadow. It is also not strictly necessary in this argument for either the sun or moon to be spheroid themselves. This is consistent with the Aristotelian (and other ancient) cosmology which has a stationary globe orbited by celestial objects. This may be regarded as a “prescientific” theory.

This is significant for our argument because it means it does not rely on knowledge ancient people did not have access to. No technology or advanced mathematics is required; it’s an argument from the flat earther’s own epistemological position of direct realism. It is something that can be observed by a single individual at a single location (or multiple individuals at multiple locations), though it does take several years of observation to establish.